Matematika kelas 10: Mei 2018

VEKTOR DI RUANG TIGA

Vektor Pada Ruang ( Dimensi 3)

Vektor di ruang 3 adalah vektor yang mempunyai 3 buah sumbu yaitu x , y , z yang saling tegak lurus dan perpotongan ketiga sumbu sebagai pangkal perhitungan.
Vektor p pada bangun ruang dapat dituliskan dalam bentuk :

koordinat kartesius p = (x, y, z)
vektor kolom p = atau, vector baris p=(x,y,z)
kombinasi linear vektor satuan i, j, k yaitu : p = xi + yj + zk

dengan i =

,j =

, dan k =

i = vektor satuan dalam arah OX
j = vektor satuan dalam arah OY
k = vektor satuan dalam arah OZ

Modulus Vektor
Modulus vektor yaitu besar atau panjang suatu vektor. Jika suatu vektor dengan koordinat titik A (x₁ , y₁ ,z₁) dan B (x₂ , y₂ , z₂) maka modulus (besar) atau panjang vektor dapat dinyatakan sebagai jarak antara titik A dan B yaitu :

Dan jika suatu vektor a disajikan dalam bentuk linear a = a₁i + a₂j + a₃k , maka modulus vektor a adalah :

Vektor Posisi

Vektor posisi titik P adalah vektor yaitu vektor yang berpangkal di titik O (0 , 0 , 0) dan berujung di titik P (x , y , z), bila ditulis

Modulus / besar vektor posisi adalah :

CONTOH SOAL VEKTOR DIMENSI DUA

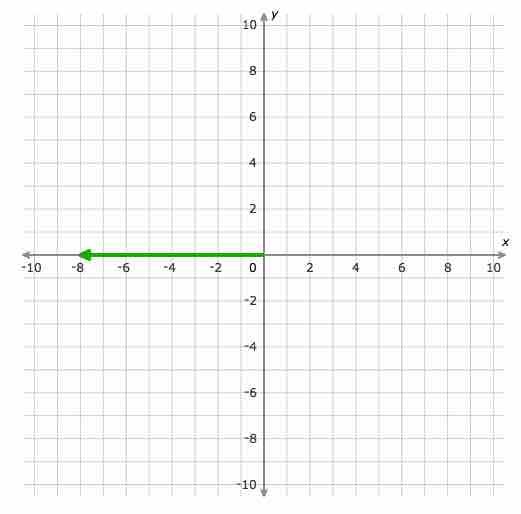1. Temukan besarnya vektor. Tulis jawaban Anda dalam bentuk yang disederhanakan:

Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.

2. Vektor-vektor u, v, dan w tak nol dan | u | = | v |, Jika | v-w | = | u-w | maka…

A. u.v = | w |
B. $w=\frac{2u+3v}{5}$
C. | u-w | = | v |
D. u – v tegak lurus w E. u + v tegak lurus w
Pembahasan:
Diketahui: | v – w | = | u – w | Kedua sisi di akarkan $\sqrt{(v-w)^2}=\sqrt{(u-w)^2}$ v.v + w.w – 2v.w = u.u + w.w – 2 u.w |v|² + |w|² – 2v.w = |u|² + |w|² – 2u.w
Dari soal diketahui | u | = | v | maka v.w = u.w u.w – v.w = 0 (u.w).w = 0 Karena perkaliannya = 0 maka (u-v) tegak lurus w.
Jawaban: D

3. Diketahui vektor-vektor $\vec{a}$ = (2, 2, z), $\vec{b}$ = (-8, y, -5) , $\vec{c}$ = (x, 4y, 4) dan $\vec{d}$ = (2x, 22, -z, 8). Jika vektor $\vec{a}$ tegak lurus dengan vektor $\vec{b}$ dan vektor $\vec{c}$ sejajar dengan $\vec{d}$ maka (y+z) =

A. -5
B. -1
C. 1
D. 2
E. 5
Pembahasan:

Jawaban: C

4. Jika vektor $\vec{a}$ dan $\vec{b}$ merupakan ( $\vec{a}$ + $\vec{b}$ ). $\vec{b}$ = 12 , | $\vec{a}$ | = 2 dan | $\vec{b}$ | = 3 maka sudut antara $\vec{a}$ dan $\vec{b}$ adalah….

A. 60°
B. 45°
C. 30⁰D. 25⁰E. 20⁰
Pembahasan:

Jawaban: A

5. Diketahui $\vec{u}=\begin{pmatrix} 3\\ -1\\ 1 \end{pmatrix}$ dan vektor $\vec{v}=\begin{pmatrix} 2\\ p\\ 2 \end{pmatrix}$ . Jika proyeksi skalar orthogonal $\vec{u}$ pada arah vektor $\vec{v}$ sama dengan setengah panjang vektor $\vec{v}$ maka nilai p = …

A. -4 atau -2
B. -4 atau 2
C. 4 atau -2
D. 8 atau -1
E. -8 atau 1
Pembahasan:

Jawaban: B

PROYEKSI VEKTOR

PROYEKSI VEKTOR

Proyeksi merupakan ilmu yang mempelajari tentang cara pandang objek dalam ruang dimensi tiga dalam gambar di ruang dimensi dua. Cara ini mempermudah kita untuk melihat objek yang terletak di ruang dimensi tiga. Pada proyeksi vektor, objek yang diproyeksikan berupa vektor, baik itu panjangnya atau vektor itu sendiri. Proyeksi dibedakan menjadi beberapa jenis, di antaranya adalah proyeksi ortogonal, aksonometri, proyeksi miring (oblique), dan perspektif. Pada pembahasan proyeksi vektor kali ini hanya akan membahas mengenai proyeksi vektor ortogonal. Jadi, untuk jenis proyeksi lainnya tidak akan dibahas pada halaman ini.

Proyeksi ortogonal adalah cara pandang mata pada sebuah objek yang ditarik garis tegak lurus pada sebuah bidang datar. Terdapat dua proyeksi ortogonal yang akan di bahas pada pembahasan kali ini, yaitu proyeksi skalar dan vektor ortogonal. Perhatikan gambar dua proyeksi vektor dengan arah yang berbeda pada gambar di bawah

Proyeksi Skalar dan Proyeksi Vektor Ortogonal

Proyeksi Skalar Ortogonal

Proyeksi skalar ortogonal biasa disebut juga dengan proyeksi panjang vektor ortogonal. Dalam kata lainnya, objek proyeksi adalah panjang vektor. Rumus untuk menghitung panjang proyeksi skalar vektor ortogonal adalah sebagai berikut.

Proyeksi skalar ortogonal $\vec{a}$ pada arah vektor $\vec{b}$ .
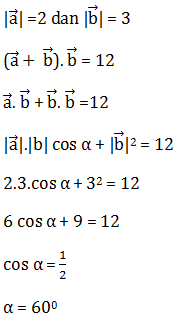
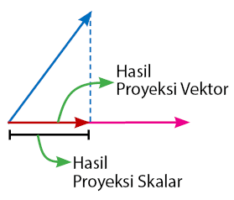
$\left| \vec{c} \right| = \frac{\vec{a} \cdot \vec{b}}{ \left| \vec{b} \right| }$
Proyeksi skalar ortogonal $\vec{b}$ pada arah vektor $\vec{a}$ .
$\left| \vec{c} \right| = \frac{\vec{a} \cdot \vec{b}}{ \left| \vec{a} \right| }$

Baca Juga: Perbandingan Vektor pada Sebuah Ruas Garis

Proyeksi Vektor Ortogonal

Objek pada proyeksi skalar vektor ortogonal adalah panjang proyeksi vektor. Sedangkan pada proyeksi vektor ortogonal yang menjadi objek utamanya adalah vektornya. Vektor hasil proyeksi dapat ditentukan melalui rumus berikut.

Proyeksi vektor ortogonal $\vec{a}$ pada $\vec{b}$ .
$\vec{c} = \frac{\vec{a} \cdot \vec{b} }{\left| \vec{b} \right| ^{2} } \cdot \vec{b}$
Proyeksi vektor ortogonal $\vec{b}$ pada $\vec{a}$ .
$\vec{c} = \frac{\vec{a} \cdot \vec{b} }{\left| \vec{a} \right| ^{2} } \cdot \vec{a}$

Contoh Soal dan Pembahasan

Panjang proyeksi ortogonal vektor $\vec{a} = (p, 2, 4)$ pada $\vec{b} = (2, p, 1)$ adalah 4. Nilai p adalah ….

$\textrm{A.} \; \; \; -4$

$\textrm{B.} \; \; \; -2$

$\textrm{C.} \; \; \; - \frac{1}{2}$

$\textrm{D.} \; \; \; \frac{1}{2}$

Pembahasan:
Mencari panjang vektor b:

$\left| \vec{b} \right| = \sqrt{2^{2} + p ^{2} + 1^{2}}$

$\left| \vec{b} \right| = \sqrt{4+ p ^{2} + 1}$

$\left| \vec{b} \right| = \sqrt{p ^{2} + 5}$

Beradasrkan rumus proyeksi skalar (proyeksi panjang) ortogonal vektor dapat diperoleh persamaan berikut.

$\left| \vec{c} \right| = \frac{\vec{a} \cdot \vec{b}}{\left| \vec{b} \right|}$

$4 = \frac{(p, 2, 4)(2, p, 1)}{\sqrt{p^{2}+5}}$

$4 = \frac{2p + 2p + 4}{\sqrt{p^{2}+5}}$

$4 = \frac{4p + 4}{\sqrt{p^{2}+5}}$

$4 = \frac{4(p + 1)}{\sqrt{p^{2}+5}}$

$1 = \frac{p + 1}{\sqrt{p^{2}+5}}$

$\sqrt{p^{2}+5} = p + 1$

$p^{2}+5 = (p + 1)^{2}$

$p^{2}+5 = p^{2} + 2p + 1$

$5 = 2p + 1$

$2p = 5 - 1$

$2p = 4 \rightarrow p=\frac{4}{2} = 2$

Jawaban: E

Matematika kelas 10

Selasa, 08 Mei 2018

VEKTOR DI RUANG TIGA

CONTOH SOAL VEKTOR DIMENSI DUA

1. Temukan besarnya vektor. Tulis jawaban Anda dalam bentuk yang disederhanakan:

2. Vektor-vektor u, v, dan w tak nol dan | u | = | v |, Jika | v-w | = | u-w | maka…

3. Diketahui vektor-vektor $\vec{a}$ = (2, 2, z), $\vec{b}$ = (-8, y, -5) , $\vec{c}$ = (x, 4y, 4) dan $\vec{d}$ = (2x, 22, -z, 8). Jika vektor $\vec{a}$ tegak lurus dengan vektor $\vec{b}$ dan vektor $\vec{c}$ sejajar dengan $\vec{d}$ maka (y+z) =

4. Jika vektor $\vec{a}$ dan $\vec{b}$ merupakan ( $\vec{a}$ + $\vec{b}$ ). $\vec{b}$ = 12 , | $\vec{a}$ | = 2 dan | $\vec{b}$ | = 3 maka sudut antara $\vec{a}$ dan $\vec{b}$ adalah….

5. Diketahui $\vec{u}=\begin{pmatrix} 3\\ -1\\ 1 \end{pmatrix}$ dan vektor $\vec{v}=\begin{pmatrix} 2\\ p\\ 2 \end{pmatrix}$ . Jika proyeksi skalar orthogonal $\vec{u}$ pada arah vektor $\vec{v}$ sama dengan setengah panjang vektor $\vec{v}$ maka nilai p = …

PROYEKSI VEKTOR

Proyeksi Skalar Ortogonal

Proyeksi Vektor Ortogonal

Contoh Soal dan Pembahasan

VEKTOR DI RUANG TIGA

Laporkan Penyalahgunaan

Selasa, 08 Mei 2018

VEKTOR DI RUANG TIGA

CONTOH SOAL VEKTOR DIMENSI DUA

1. Temukan besarnya vektor. Tulis jawaban Anda dalam bentuk yang disederhanakan:

2. Vektor-vektor u, v, dan w tak nol dan | u | = | v |, Jika | v-w | = | u-w | maka…

3. Diketahui vektor-vektor = (2, 2, z), = (-8, y, -5) , = (x, 4y, 4) dan = (2x, 22, -z, 8). Jika vektor tegak lurus dengan vektor dan vektor sejajar dengan maka (y+z) =

4. Jika vektor dan merupakan ( + ). = 12 , || = 2 dan || = 3 maka sudut antara dan adalah….

5. Diketahui dan vektor . Jika proyeksi skalar orthogonal pada arah vektor sama dengan setengah panjang vektor maka nilai p = …

PROYEKSI VEKTOR

Proyeksi Skalar Ortogonal

Proyeksi Vektor Ortogonal

Contoh Soal dan Pembahasan

VEKTOR DI RUANG TIGA

3. Diketahui vektor-vektor $\vec{a}$ = (2, 2, z), $\vec{b}$ = (-8, y, -5) , $\vec{c}$ = (x, 4y, 4) dan $\vec{d}$ = (2x, 22, -z, 8). Jika vektor $\vec{a}$ tegak lurus dengan vektor $\vec{b}$ dan vektor $\vec{c}$ sejajar dengan $\vec{d}$ maka (y+z) =

4. Jika vektor $\vec{a}$ dan $\vec{b}$ merupakan ( $\vec{a}$ + $\vec{b}$ ). $\vec{b}$ = 12 , | $\vec{a}$ | = 2 dan | $\vec{b}$ | = 3 maka sudut antara $\vec{a}$ dan $\vec{b}$ adalah….

5. Diketahui $\vec{u}=\begin{pmatrix} 3\\ -1\\ 1 \end{pmatrix}$ dan vektor $\vec{v}=\begin{pmatrix} 2\\ p\\ 2 \end{pmatrix}$ . Jika proyeksi skalar orthogonal $\vec{u}$ pada arah vektor $\vec{v}$ sama dengan setengah panjang vektor $\vec{v}$ maka nilai p = …